Statistics Terms
Logit Link Function
220799a and mcfad2me
Analogy
Imagine that you are attending an international conference where conference attendees speak a variety of different languages. You need to communicate throughout the conference with a colleague, but you speak different languages. You could try to directly translate each word or phrase from one language to another to communicate, but this may not be the most interpretable form of communication. Instead, you could bring in a skilled translator who is fluent in both languages. This translator acts as a link between the two languages, converting the message from one language to another while ensuring that the meaning remains intact.
Diagram
The diagram below illustrates how a link function can transform data into a linear relationship. In statistics, we sometimes have relationships between variables that make direct comparison challenging. In logistic regression, we are interested in predicting the probability of a binary outcome based on one or more predictor variables. However, the probability of a binary outcome does not have a linear relationship with the predictor variable(s). The link function that is used for binary outcomes is the logit function. The logit link function is used to linearly model the relationship between predictors and the log-odds of the outcome.
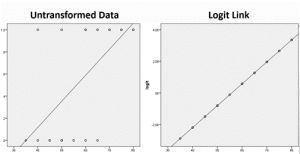
Transforming the distribution of the binary outcome to the log-odds of the outcome converts the relationship between variables into a form that is more interpretable or suitable for analysis. You may be wondering “is log-odds really an interpretable outcome?”. The good news is that there are simple conversions from log-odds to odds and from odds to probabilities for simple interpretations of parameters after running a logistic regression model.
Example
A researcher is interested in predicting the probability of young people voting based on age, gender, income, SES, and political affiliation. The probability of young people voting is bounded between 0 and 1, so in order to predict the outcome, the researcher must use a link function. Here, with a binary outcome variable, the researcher should use a logit link function. This would transform the outcome to a scale that ranges from negative infinity to positive infinity so that the outcome is no longer bounded and can be modeled linearly.
After running the analysis, the researcher is having a hard time interpreting the parameter estimates on the log-odds metric. So, he transforms the log-odds outcome parameters to odds. Now, the researcher can easily interpret his outcome.
For example, for SES, the researcher may see that for every one unit increase in SES, there is an XX increase in log-odds of voting. That is not very interpretable! After converting the outcome parameter estimates to odds, the researcher can now say that for every one unit increase in SES, the odds of voting will increase by a factor of XX.
The transformation of log-odds to odds is: Odds=elogit(p); that is, you take the natural antilog of the log-odds in order to compute odds for easier interpretability.
Plain Language Definition
The logit link function is how a binary outcome gets transformed into something that can be modeled as a linear function of the predictors.
Technical Definition
The logit link function is a function that connects the binary outcome to the linear predictor variable(s). Mathematically, the logit link function g(⋅) can be defined as:
g(η) = logit(p) = ln(p/1−p)
where:
- logit(p) is the log-odds of the probability of 1
- p is the probability of 1
Media Attributions
- adept2

