The flow of a program is often controlled using one or more flags, which are binary values (i.e., yes/no, on/off, true/false) that indicate the current or desired state of the system. This chapter considers one common approach for working with flags.

Motivation

Suppose you’re developing an adventure game in which there are a variety of different items that players can collect and put in their inventory, and the actions that players can take (and the results of those actions) depend on the items that they have in their possession. Without knowing anything else about the game, it’s clear that the program will include a variety of if statements that will control the flow, and that these if statements will have boolean expressions that involve the variables that represent the items. This chapter will help you solve problems that involve the management of, and the performance of operations on, these kinds of variables.

Review

You could, of course, have a boolean variable for each item that is assigned true when the player has the item and false otherwise. The shortcoming of this approach is that there tends to be a large number of such variables, and they all need to be passed into the various methods that need them.^[1]

Thinking About The Problem

Bit flags take advantage of the fact that everything in a digital computer is stored as 0s and 1s. For example, suppose a non-negative integer is represented by 4 bits, each of which can contain a 0 or 1. Each of the 4 positions corresponds to a power of 2 (i.e., the 1s place, the 2s place, the 4s place, and the 8s place). This is illustrated in Figure 10.1 for the 4-bit binary number 1101, which is 13 in base 10. (If you’re confused, see Figure 3.1 for an example that uses base 10.)

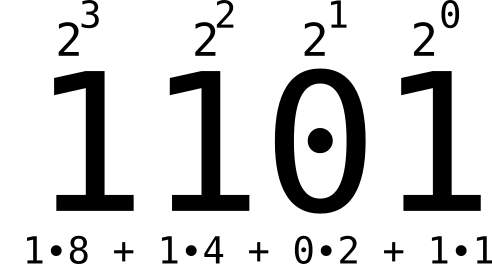
Given this representational scheme, you can use a single non-negative 4-bit integer to hold up to four different binary flags. Then, you can use the &, |, and ^ operators to perform bitwise “and”, “inclusive or”, and “exclusive or” operations on these integer values.

The Pattern

For simplicity, assume that the number of flags you need to work with can be represented using a single variable (e.g., one int or long). The pattern then involves several steps:

1. Create masks that represent each of the binary states of interest. Each mask is a variable of appropriate type that is initialized to a unique power of 2.
2. Declare a variable that will hold the bit flags.
3. As needed, set particular bits (i.e., make the bits 1) using the | operator, clear particular bits (i.e., make the bits 0) using the & operator, and/or toggle particular bits (i.e., switch the bits to their other value) using the ^ operator.
4. As needed, check the value of particular bit using the | operator and a relational operator.

The way in which you should check the value of particular bit flags varies with what you are trying to accomplish. However, before considering those details, it is important to think about how you can combine simple masks into composite masks.

Again for simplicity, suppose that the variables you are using are represented using eight bits and that the left-most bit is used to indicate the sign (with a 0 indicating that the number is positive). Then, there are seven different unique (positive) masks, as follows: 00000001, 00000010, 00000100, 00001000, 00010000, 00100000, and 01000000, each of which has a single bit that is set. You can create a composite mask (i.e., a mask with more than one bit set) using the | operator. For example, suppose you want a composite mask with both the left-most usable bit and the right-most bit set. You can accomplish this as follows:

[latex]\begin{align*} & \texttt{00000001} \\ \texttt{ | } & \texttt{01000000} \\ \hline & \texttt{01000001} \end{align*}[/latex]

Now, suppose you have a composite mask named needed and a state variable named actual. There are several things you might want to know about the relationship between the two, and each question must be answered slightly differently.

Suppose you want to know if any of the bits that are set in needed are also set in actual. You can accomplish this as follows:

    public static boolean anyOf(int needed, int actual) {
        return (needed & actual) > 0;
    }

The expression needed & actual evaluates to a value in which a particular bit in that value is set if and only if the corresponding bit is set in both needed and actual. Then, if any bit in needed & actual is set, the expression (needed & actual) > 0 will evaluate to true.

Instead, you might want to know if all of the bits that are set in needed are also set in actual. You can accomplish this as follows:

    public static boolean allOf(int needed, int actual) {
        return (needed & actual) == needed;
    }

Finally, you might want to know if exactly the same bits in needed and actual are set. This can be accomplished as follows:

    public static boolean onlyOf(int needed, int actual) {
        return (needed == actual);
    }

That is, needed and actual must be identical.

Examples

Returning to the example of the adventure game, you can represent the individual items using the following masks:

    public static final int FOOD   =  1;
    public static final int SPELL  =  2;
    public static final int POTION =  4;
    public static final int WAND   =  8;
    public static final int WATER  = 16;   
    // And so on...

You can then represent the player’s inventory as a single int as follows:

        int inventory;
        inventory = 0;

When the player acquires an individual item, you can use the bitwise “or” operator to adjust the inventory. For example, suppose the player acquires WATER. You can use the updating pattern from Chapter 1 as follows:

        inventory = inventory | WATER;

At this point, the variable inventory contains the value 16. But, what’s important is that the bit corresponding to “having water” is set.

Suppose the player later acquires SPELL. You can handle this as follows (using the compound assignment operator in this case, to illustrate its use):

        inventory |= SPELL;

At this point, the variable inventory contains the value 18. But, again, what’s important is that the bits corresponding to “having spell” and “having water” are set.

You can then check to see if the bit corresponding to “having water” is set as follows:

        boolean haveWater = (inventory & WATER) > 0;

Note that either the allOf() algorithm or the anyOf() algorithm would work in this case, since the mask is not composite.

Similarly, you can then check to see if the bit corresponding to “having a potion” is set as follows:

        boolean havePotion = (inventory & POTION) > 0;

When the player later drinks the water, you can clear that bit as follows:

        inventory = inventory & (WATER ^ Integer.MAX_VALUE);

Here, since Integer.MAX_VALUE is an int in which every bit is 1 (except for the sign bit), the result of (WATER ^ Integer.MAX_VALUE) is a mask in which all of the bits of WATER (except the sign bit) have been toggled. This is easy to see using 8-bit int values as follows:

[latex]\begin{align*} & \texttt{00010000} \\ \texttt{ ^ } & \texttt{01111111} \\ \hline & \texttt{01101111} \end{align*}[/latex]

So, since the bit that corresponds to water in this new mask is 0, The bitwise & of inventory with this new mask will clear the bit that corresponds to water in the result.

Some Warnings

Note that beginning programmers commonly use the wrong bitwise operator when creating composite masks. This is because they tend to describe the process as setting one bit and another bit. However, if you take the bitwise & of two simple masks, the result will always be zero. For example, consider the 8-bit representations of the mask for food and the mask for water. Suppose you want to create a composite mask to determine if the player has both food and water. If you create the mask using the bitwise & operator, you get the following:

[latex]\begin{align*} & \texttt{00000001} \\ \texttt{ & } & \texttt{00010000} \\ \hline & \texttt{00000000} \end{align*}[/latex]

If, instead, you use the bitwise | operator, you get the desired result, as follows:

[latex]\begin{align*} & \texttt{00000001} \\ \texttt{ | } & \texttt{00010000} \\ \hline & \texttt{00010001} \end{align*}[/latex]

Note that beginning programmers also make the same mistake when updating the variable that contains the current state. Again, using 8-bit representations, suppose the player has water. Then inventory will be 00010000. When the player later acquires the spell, you must use the bitwise | operator as follows:

[latex]\begin{align*} & \texttt{00010000} \\ \texttt{ | } & \texttt{00000010} \\ \hline & \texttt{00010010} \end{align*}[/latex]

If you used the bitwise & operator (thinking the player has water and the spell), you would wind up with nothing in inventory. This can be shown as follows:

[latex]\begin{align*} & \texttt{00010000} \\ \texttt{ & } & \texttt{00000010} \\ \hline & \texttt{00000000} \end{align*}[/latex]

Looking Ahead

At this point, it is sufficient to think that integer values are represented in a specified number of bits with the left-most bit indicating the sign (0 for positive values and 1 for negative values). In fact, this is not the representational scheme that is used most commonly. One easily understood problem with such a scheme is that there are two different representations of zero. Using eight bits, this scheme has both positive zero (i.e., 00000000) and negative zero (i.e., 10000000). When you take a deeper look at data types, you will learn that the most common representation of integers is a system called two’s complement. This system works essentially like an odometer, with a single zero (i.e., 00000000) that rolls up to the first positive integer (i.e., 00000001) and rolls back to the first negative integer (i.e., 11111111). This means that there is one more negative number than there are positive numbers. Fortunately, the left-most bit of all negative numbers is still 1 and the left-most bit of all positive numbers is still 0.

If, in the future, you take a course on data structures and algorithms you may also learn about the BitSet class which allows the number of flags to “grow”. In particular, you may consider the time and space efficiency of providing this functionality.